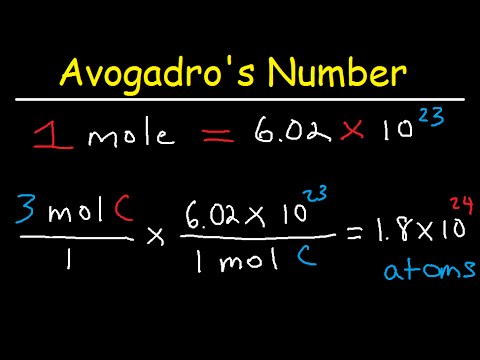The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons's law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles's law). The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle's law).
Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro's law). We will consider the key developments in individual relationships , then put them together in the ideal gas law. Gases whose properties of P, V, and T are accurately described by the ideal gas law are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter.
To get to moles, use the equation and the molar ratios shown. To get to volume, use the molar volume of gas constants. To get to mass, use the atomic/molecular masses shown in the periodic table. Hydrogen gas has the chemical formula H2 and the molecular weight of 2. This gas is the lightest substance among all chemical compounds and the most abundant element in the universe.
Hydrogen gas has also drawn significant attention as a potential energy source. Hydrogen can be obtained, for example, by electrolysis of the water. You calculate the amount of hydrogen in moles either from the gas mass or using the ideal gas law.
At room temperatures, collisions between atoms and molecules can be ignored. In this case, the gas is called an ideal gas, in which case the relationship between the pressure, volume, and temperature is given by the equation of state called the ideal gas law. The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm.
If the temperature is in kelvin, volume and temperature are directly proportional. Charles's law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant. The molar volume of gas at STP, standard temperature and pressure (0°C or 273K, 100 kPa pressure) is 22.4 litres per mole (22.4 L/mol). In other words, one mole of atoms of a pure ideal gas at 0°C will fill 22.4 litres of space. The molar volume of gas at room temperature (25°C, 298K) and pressure is 24 litres per mole (24 L/mol). Examples and practice problems of solving equation stoichiometry questions with gases.
We calculate moles with 22.4 L at STP, and use molar mass and mole ratios to figure out how many products or reactants we have. The ideal gas law can be considered to be another manifestation of the law of conservation of energy . Work done on a gas results in an increase in its energy, increasing pressure and/or temperature, or decreasing volume. This increased energy can also be viewed as increased internal kinetic energy, given the gas's atoms and molecules. The most common molar volume is the molar volume of an ideal gas at standard temperature and pressure (273 K and 1.00 atm).
Atoms and molecules are close together in solids and liquids. Thus gases have lower densities than liquids and solids. Density is mass per unit volume, and volume is related to the size of a body cubed. So if the distance between atoms and molecules increases by a factor of 10, then the volume occupied increases by a factor of 1000, and the density decreases by a factor of 1000. Use the ideal gas law to calculate pressure change, temperature change, volume change, or the number of molecules or moles in a given volume. To recall the molar volume of gas at standard temperature and pressure and its meaning.
Multiply the volume and pressure and divide the product by the temperature and the molar gas constant to calculate moles of the hydrogen gas. One mole always contains 6.02 × 1023 particles , independent of the element or substance. A mole of any substance has a mass in grams equal to its molecular mass, which can be calculated from the atomic masses given in the periodic table of elements. The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises. Read on to find out more about the ideal gas law, moles, and examples & tips on how to resolve chemical equations.
The ideal gas law relates the pressure and volume of a gas to the number of gas molecules and the temperature of the gas. Calculate the number of molecules in a cubic meter of gas at standard temperature and pressure , which is defined to be 0ºC and atmospheric pressure. The final temperature is about 6% greater than the original temperature, so the final pressure is about 6% greater as well. Note that absolute pressure and absolute temperature must be used in the ideal gas law.
The answer lies in the large separation of atoms and molecules in gases, compared to their sizes, as illustrated in Figure 2. Because atoms and molecules have large separations, forces between them can be ignored, except when they collide with each other during collisions. The motion of atoms and molecules is fast, such that the gas occupies all of the accessible volume and the expansion of gases is rapid. In contrast, in liquids and solids, atoms and molecules are closer together and are quite sensitive to the forces between them.
In another lesson, you learned about ideal gases and the ideal gas equation. Ideal gases are just what they sound like - ideal. If we partially fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa.
Volume-pressure data for an air sample at room temperature are graphed in Figure 5. Methods to calculate number of moles of chemicals in reactions using mass, moles and volume of gas. Use the mass of the hydrogen gas to calculate the gas moles directly; divide the hydrogen weight by its molar mass of 2 g/mole.
The molar volume is the volume occupied by one mole of a substance at a given temperature and pressure. Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm3 when immersed in a mixture of ice and water (0.00 °C). When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm3. Find the temperature of boiling ammonia on the kelvin and Celsius scales.
Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the sphere, the gas inside gets hotter and the pressure increases.
This calculator allows you to input the data you have in any order you wish - so don't stress if you know the molar mass but not the pressure! Our extensive range of units will enable you to calculate the desired value without hassle; you won't have to leave this page! It also provides you with an opportunity to change all the values on the go. A mole of any substance has a mass in grams equal to its molecular weight, which can be determined from the periodic table of elements.
How many molecules are in a typical object, such as gas in a tire or water in a drink? We can use the ideal gas law to give us an idea of how large N typically is. We calculate moles with the Ideal Gas Law, because the conditions are not at STP, and use molar mass and mole ratios to figure out how many products or reactants we have. 1 mole of every gas occupies the same volume, at the same temperature and pressure. Determine the moles of the gas using the ideal gas law equation.
At the same temperature and pressure equal volumes of all gasses contain the same number of molecules. Dn is the difference in the number of moles of gases on each side of the balanced equation for the reaction. What is the gauge pressure in a 25.0ºC car tire containing 3.60 mol of gas in a 30.0 L volume? What will its gauge pressure be if you add 1.00 L of gas originally at atmospheric pressure and 25.0ºC? Assume the temperature returns to 25.0ºC and the volume remains constant. State the ideal gas law in terms of molecules and in terms of moles.
For those reasons, scientists often try to find a way to "linearize" their data. If we plot P versus V, we obtain a hyperbola . Calculate the change in the number of moles of gases, Dn. Calculate the change in the number of moles of gases.
We know that in this reaction, one mole of CH4 reacts with two moles of O2. CH4 has a molar mass of 16 grams per mol (g mol-1) and O2 has a molar mass of 32 grams per mole. Liquids and solids have densities about 1000 times greater than gases.
Explain how this implies that the distances between atoms and molecules in gases are about 10 times greater than the size of their atoms and molecules. Substitute the known quantities, along with their units, into the appropriate equation, and obtain numerical solutions complete with units. Be certain to use absolute temperature and absolute pressure.
Solve the ideal gas law for the quantity to be determined . You may need to take a ratio of final states to initial states to eliminate the unknown quantities that are kept fixed. Let us now examine the role of energy in the behavior of gases.
When you inflate a bike tire by hand, you do work by repeatedly exerting a force through a distance. This energy goes into increasing the pressure of air inside the tire and increasing the temperature of the pump and the air. We first need to calculate the molar mass of acetaminophen. To do this, we need to multiply the number of atoms of each element by the element's atomic mass. Atoms and molecules in a gas are typically widely separated, as shown. Converting Kc to KpCalculate the difference in the number of moles of gases.
To convert between Kc to Kp use the following equation which is based on the relationship between molarities and gas pressures. First you want to make sure all of your units are consistent with the molar mass constant so your units will cancel. Calculate the volume and number of moles of reactants involved in chemical reactions.
The pressure in the tire is changing only because of changes in temperature. First we need to identify what we know and what we want to know, and then identify an equation to solve for the unknown. Suppose your bicycle tire is fully inflated, with an absolute pressure of 7.00 × 105 Pa (a gauge pressure of just under 90.0 lb/in2) at a temperature of 18.0ºC. What is the pressure after its temperature has risen to 35.0ºC?
Assume that there are no appreciable leaks or changes in volume. From the equation for a reaction, we can tell how many moles of a gas take part. Using Avogadro's Law, we can also work out its volume.
Calculate the volume of carbon dioxide gas, CO2, occupied by 5 moles and 0.5 moles of the gas occupied at STP. A 15.0-L sample of carbon dioxide, at 742 mm Hg and 10.degree C, is changed to 778 mm Hg and 40 degree C. Standard pressure, expressed in mm Hg, is 760 mm Hg. Calculate the pressure in bar of 2520 moles of hydrogen gas stored at 27 °C in the 180-L storage tank of a modern hydrogen-powered car.
This answer supports our expectation from Charles's law, namely, that raising the gas temperature at a constant pressure will yield an increase in its volume (from 0.300 L to 0.321 L). While we can use mass to find number of moles, we need another relation for gases because it is often quite impractical to measure the mass of a gas. Gases are much easier to measure by their volume, or the amount of 3d space they occupy.
The molar mass of a gas is significant in calculations of Graham's law of diffusion. Molar mass is often confused with atomic or molecular mass. Although their values are identical, they describe different quantities. The ideal gas law is generally valid at temperatures well above the boiling temperature.
This number is undeniably large, considering that a gas is mostly empty space. For example, 1 cm3of a gas at STP has 2.68 × 1019 molecules in it. Once again, note that N is the same for all types or mixtures of gases. When air is pumped into a deflated tire, its volume first increases without much increase in pressure.